Pytorch 04) - Deep Nueral Network

Pytorch - 04) Deep Neural Network

Deep Neural Network

이전 Perceptron에서 한개의 Perceptron으로는 XOR연산을 효과적으로 분류하지 못한다는 것을 이야기 했었다.

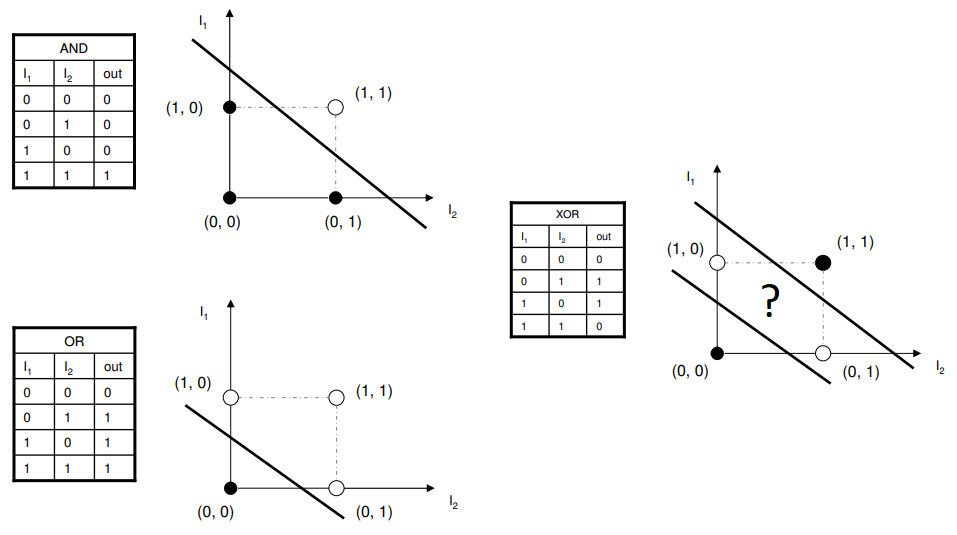
그리고 이런 XOR 이 아니더라도, 선형이 아닌 형태의 데이터를 분류 할 수 없을 것이다.

이런형태의 데이터는 어떻게 classification 해야 될까? 라는 생가에서 시작된게, perceptron을 여러개 배치하는 것이다.

Tensorflow playground 예제다.

input layer 와 output layer 사이에 4개의 perceptron을 배치했는데, 각각의 perceptron이 선형으로 되어 있으며, 이 4개의 선형이 이루는 사각형 형태로 classification이 되어 있음을 알 수 있다.

$x1, x2$에 대한 입력값이 각각 있고, 이 입력 값에 대해서 서로다른 perceptron이 다른 weight을 바탕으로 각각 다른 구별을 하고, 이 두가지 값을 또다른 weight로 보는 작업들을 반복하여 작업을 수행한다.

Feedforward

input layer의 값이 hidden layer 로 전달되고, hidden layer가 ouput layer로 전파하는 과정 (hidden layer가 여러개면 hidden layer간 전파도 있을 것이다)을 feedforward, 순전파라고 한다. 말그대로, 앞쪽의 입력값을 뒤로 보내는 것을 의미한다. hidden layer에 있는 각각의 노드는 퍼셉트론의 활성함수라고 볼 수 있다.

Backpropagation

임의의 값을 기반으로 보낸 feedforward가 당연히 제대로된 classification을 해낼리가 없다. 그래서 Backpropagation(역전파)를 한다. 역전파는 input의 역방향으로 오차를 돌려보내서 weight을 재업데이트 하는 것이다. 각 파라미터 별로 Loss에 대한 그래디언트를 구한뒤, 그래디언트들이 향한 쪽으로 파라미터를 업데이트 한다.

Code

데이터셋

import torch
import numpy as np
import matplotlib.pyplot as plt
import torch.nn as nn
from sklearn import datasets

n_pts = 500
X, y = datasets.make_circles(n_samples=n_pts, random_state=123, noise=0.2, factor=0.3)

x_data = torch.Tensor(X)
y_data = torch.Tensor(y.reshape(500, 1))

def scatter_plot():
  plt.scatter(X[y==0, 0], X[y==0, 1], color='red')
  plt.scatter(X[y==1, 0], X[y==1, 1], color='blue')

scatter_plot()

가운데 파란색 점들이 1이고, 빨간색이 0 이다.

class Model(nn.Module):

  def __init__(self, input_size, H1, output_size):
    super().__init__()
    self.linear1 = nn.Linear(input_size, H1)
    self.linear2 = nn.Linear(H1, output_size)

  def forward(self, x):
    x = torch.sigmoid(self.linear1(x))
    x = torch.sigmoid(self.linear2(x))
    return x

  def predict(self, x):
    return 1 if self.forward(x) >= 0.5 else 0

차이점은 hidden layer가 하나 추가됐다는 것이다. 두개 모두 linear로 처리되고 있으며, 활성화 함수로 sigmoid를 적용하였다.

model = Model(2, 4, 1)
print(list(model.parameters()))

input, hidden, output이 각각 2, 4, 1 이다.

[Parameter containing:
tensor([[-0.1573,  0.6670],
        [-0.5144,  0.6607],
        [ 0.6625,  0.1984],
        [ 0.3064, -0.2649]], requires_grad=True), Parameter containing:
tensor([-0.0411,  0.6752, -0.0167,  0.6902], requires_grad=True), Parameter containing:
tensor([[-0.2804, -0.0074,  0.1881,  0.4310]], requires_grad=True), Parameter containing:
tensor([-0.1316], requires_grad=True)]

이제 학습을 시켜보자.

criterion = nn.BCELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

epochs = 1000
losses = []

for i in range(epochs):
  y_pred = model.forward(x_data)
  loss = criterion(y_pred, y_data)

  print("epochs:", i, "loss:", loss.item())

  losses.append(loss.item())
  optimizer.zero_grad()
  loss.backward()
  optimizer.step()

epochs: 0 loss: 0.6942843198776245
epochs: 1 loss: 0.6935287117958069
epochs: 2 loss: 0.6930914521217346
epochs: 3 loss: 0.6929344534873962
epochs: 4 loss: 0.6929613351821899
epochs: 5 loss: 0.6930437088012695
epochs: 6 loss: 0.6930822730064392
epochs: 7 loss: 0.6930424571037292
epochs: 8 loss: 0.6929377913475037
epochs: 9 loss: 0.6928017139434814
...
epochs: 990 loss: 0.12231576442718506
epochs: 991 loss: 0.12226035445928574
epochs: 992 loss: 0.12220513820648193
epochs: 993 loss: 0.12215007096529007
epochs: 994 loss: 0.12209513783454895
epochs: 995 loss: 0.12204025685787201
epochs: 996 loss: 0.12198563665151596
epochs: 997 loss: 0.12193109095096588
epochs: 998 loss: 0.12187661975622177
epochs: 999 loss: 0.1218223124742508

plt.plot(range(epochs), losses)

오차가 완만하게 감소하여 약 0.1에서 수렴함을 알수 있다.

def plot_decision_boundray(X, y):
  # x축 y축 min max 값을 구해 그래프의 상하좌우 길이를 세팅한다.
  x_span = np.linspace(min(X[:, 0]), max(X[:, 0]))
  y_span = np.linspace(min(X[:, 1]), max(X[:, 1]))
  # 이 두개로 그리드를 만든다.
  xx, yy = np.meshgrid(x_span, y_span)
  # .ravel()로 평탄화 하고 이 둘을 합쳐 tensor로 변환한다.
  grid = torch.Tensor(np.c_[xx.ravel(), yy.ravel()])
  # 값 예측
  pred_func = model.forward(grid)
  # xx와 모양을 맞춰 그래프에 넣을 수 있게 세팅한다.
  # detach를 하여 autograd를 off한다.
  # numpy()로 변환하여 그래프를 그릴 수 있게 한다.
  z = pred_func.view(xx.shape).detach().numpy()
  # 등고선
  plt.contourf(xx, yy, z)

그래프가 완성되었다. 짙은 검은색일 수록 1일 확률이 높고, 그렇지 않은 영역은 하얀색에 가깝다. 대체로 overfitting되지 않고 제대로 예측한 것을 알 수 있다.